此文内容整理自Coursera课程文本检索与搜索引擎（Text Retrieval and Search Engines）。

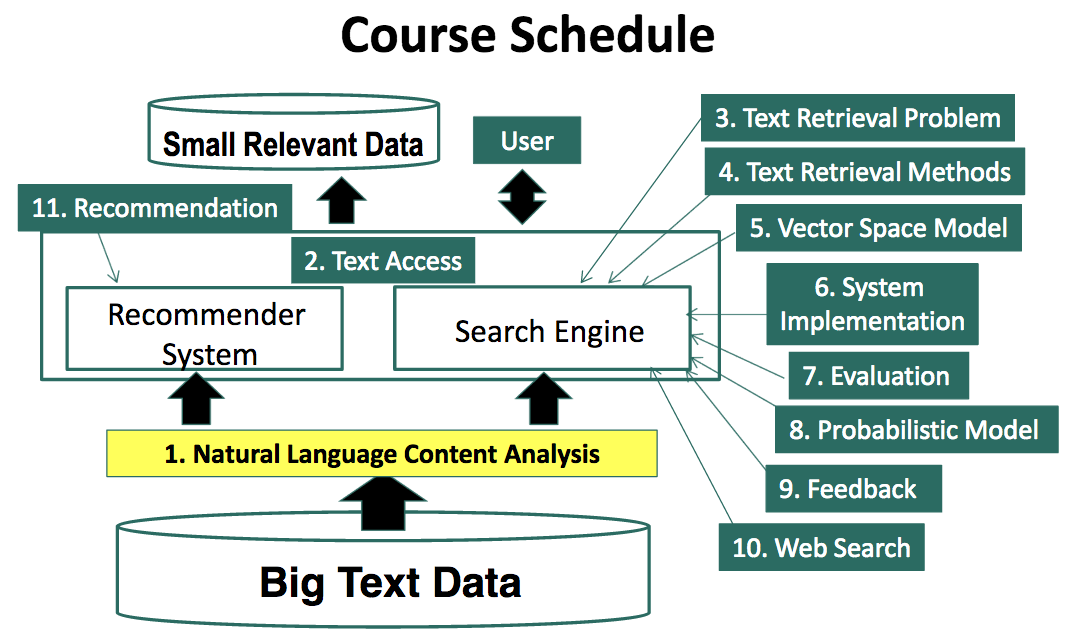
课程结构

术语表

• Text Retrieval（TR）：文本检索
• Information Retrieval（IR）：信息检索
• Natural Language Processing（NLP）：自然语言处理
• Information Need：信息需求
• Document：文档
• Query：查询
• Relevance：相关度
• Similarity：相似度
• Ranking Function：排序函数
• Vector Space Model（VSM）：向量空间模型
• Term：关键词（文档中的基本概念），可以是词、短语或ngram等
• Bag of Words（BOW）：词袋
• Bit Vector：位向量
• Dot Product：点积

序言（葛剑雄）

本书每一章都以一个具体的历史事件或人物开始，引出相应地理论、概念或方法。

尽管对不熟悉西方历史背景的中国读者来说，这些内容显得陌生。

“历史是一个过程、一种论辩，是由关于过去的真实故事所构成的。”

历史上的故事有很多，我们会挑哪些出来讲？以哪种方式来回想？讲述的效果如何？凡此种种，都带给我们一个问题——历史是为了什么，或为了谁？

过去的历史被编纂出来，“历史服务于一个目的：给人们以认同感。在这个意义上，它就像记忆一样，但它是谁的记忆？有哪些事情需要记忆？

原始证据与”二手“资料

“历史学家能否理解和接近过去的生活？他们写下的故事是否是’真实的故事’？历史的意义会是什么？”

“为何要研究历史，历史何以重要”的三个理由。（认识到以不同方式行事的可能性：避免想当然，比如对于同性恋的看法。）

误区

1. 同时做太多事情
2. 过于相信自己的意志力
3. 或期待一种完美的状态，在此状态下，甚至不需要意志力，自己”应该“知道想做什么（而且是100%地知道）

可能是npm的问题，也可能是Hexo的问题，总之：

• Error: Cannot find module ’./build/Release/DTraceProviderBindings’频繁出现
• 将网站从一个目录移动到另一个目录也颇需要一番周折

可参考的两篇文章：

• mac osx 下 hexo DTraceProviderBindings 错误

• The note of how to rebuild hexo+next blogs when switch to another PC or reinstall system

PS：不熟悉Node.js，每次安装都莫名担心会失败。。。

PPS：测试git commit效果。

PPPS：测试Github Pages更新。

Languages I am living with:

• Python
• Scala
• C#

Languages I am falling in love with:

• Racket/Scheme
• OCaml
• Julia
• Rust

Syntax Highlits

Python

1

print("Hello, World!")

Scala

1
2
3

object HelloWorld extends App {
  println("Hello, World!")
}

MathJax

Inline

Euler’s identity: e^iπ + 1 = 0.

Block (Euler’s formula)

e^iπ = cosx + isinx